■■数学めがね ○-○ ■■
「数学の話題が見える」というメガネで自分のまわりを見てみました。
疑問や質問、面白い数学っぽい話題話を自己流で紹介します。○-○
【中学３年の問題】
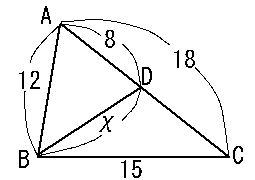
生徒から質問された問題です。うまく相似に気づくことが大切です。でも「２組の辺の比とその間の角が
それぞれ等しい」という相似条件で相似を見つけることは結構難しいようです。もし気づかなかった時は、
相似を使わず三平方の定理で解くこともできます。チャレンジしてみてください。
【差の三角形を完成してみよう】
講演の中に出てきた問題です。下の三角形の○の中に１から６までの全ての整数を入れ、２段目３段目が
上の二つの数の差になっているようにしたい。○の中に６つの整数をどのように入れればいいでしょうか。
簡単ですがちょっと考える問題としては面白いと思います。
○○○
○○
○
解答例はこちらです
【難しいでも楽しい「難解迷路体験」】
普通の迷路ではなく分かれ道に制限がある迷路です。下の図のようにとがった角を曲がることはできません。
 |
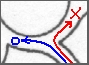この迷路は「算数数学パズルランド」というイベントで知りました。
始めは簡単そうに思えましたが・・結構難しい先の読めない迷路でした。
迷路とは、人本来の好奇心を引き出してくれるパズルの王様のようです。
私も３２分間このパズルに没頭しました。さあ、あなたはできますか？
ヒントは、とがっている分かれ道に注目することです。 |
【比例、反比例の少し難しい問題】
比例に関する難しい問題を紹介します。
○「y+5 は 3x-1 に比例し、x=1 のとき y=-1 となる。このときyをxの式で表しなさい」
という問題です。中学校１年生には少し難しい問題です。
解答は 比例ですから求める式は、y+5=a(3x-1) という式になります。x=1のとき
y=-1なので式に代入して-1+5=a(3-1)となり、その式を満たすaの値は2となり、式は
y+5=2(3x-1)。すなわちy=6x-7となります。
○「毎日６人ずつ働くと１２日で終わる仕事がある。この仕事をx人ずつ働いてy日で終わったとして
yをxの式で表しなさい」
解答は6人で12日かかる仕事なので全仕事量は6×12=72と表される。この仕事をx人でやるので
y=72/x という式で表される。この72の意味を教えることは少し難しい。（生徒はこの７２を
１人でこの仕事をやるときにかかる日数と教えてくれました）
【一見複雑な展開ですが・・】
（x－a)(x－ｂ)(x－c)(x－d)(x－e)(x－f)・・・・(x－y)(x－z) を展開するとどうなりますか。
一瞬これは大変と思いますが以外に答えは０と簡単なもの。(x－x)=0となるためです。面白い話題です。
（研究会での話題です）
【色々な数当てマジックカード】
相手にカードを１枚ずつ見せ、意中の数字が「ある」「ない」だけをこたえさせ、その結果だけ
で即座にその数を当てる。当てられたとき相手はとてもびっくりするでしょう。「なぜ」という疑問が
自然と湧いてきます。知的好奇心をくすぐる数当てマジックカード。・・さあその当て方は？ 考えてみてください。
【①１から６３までの整数を６枚のカードであてる。その方法は？】
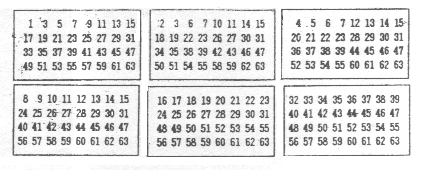
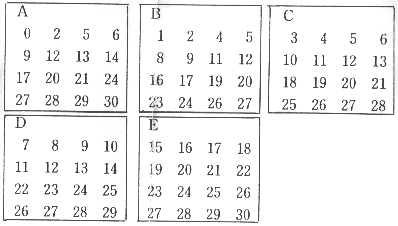
【②０から３０までの整数を５枚のカードでズバリ当てるカード。そのやり方は？】
やり方を見たい人はこちらへ
【手作り知恵の輪の紹介】
自分で知恵の輪を作成することはとても楽しいです。知恵の輪やパズルの素材研究は、授業などの
教材作成にもとても参考になります。ただ頭の中だけでの数学だけではなく、やはり触って試行錯誤し
て思考を広げていく数学の素材が必要でしょう。自作の知恵の輪は市販品にはない愛着がわいてきます。
【チェーンをはずす知恵の輪（これも面白い）】
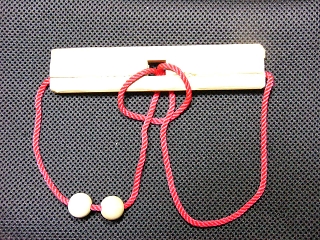
【２つの球を同じ側に集めるパズル（球は四角の穴に通らない。さあどうやれば）】
紐のパズルは複雑で金属の知恵の輪よりもわかりにくい
↓（このように球が同じ側にくるようにする）
【手作り知恵の輪（ハートをはずせ）】
お気に入りの知恵の輪は下の知恵の輪です。これもステンレスの針金で作成しました。作成に
少しペンチと格闘しなければいけませんが、ステンレスの針金は型くずれがせず自作の知恵の輪
を作成するにはもってこいの材質です。この知恵の輪はわかればいとも簡単にはずせるところが
とても魅力的。また、この知恵の輪ができるようになると「だからハートの形なんだ」と納得でき
ます。
その解き方の動画はこちら
【手作りチャイニーズリング】
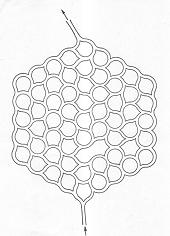
リングが連なっていて複雑に絡み合っている下のような知恵の輪をチャイニーズリングという
そうです。大学が企画している「算数・数学サロン」でそのチャイニーズリングと出会い
とても興味をもちました。その状況の複雑さと操作の単純さがとても魅力的な知恵の輪です。
解法のキーワードは「お隣のリングが大切」と教えてもらいました。そのついでにこのチャイ
ニーズリングを自作量産に成功しました。材料はホームセンターでステンレス製の針金、リング
穴あきの金の板、木片、銅の釘（長めのもの）でＯＫです。以外と簡単です。一挙に５つ作成し
ました。
解き方のヒント動画
【建物が数学っぽい・綺麗】
新宿の東京都庁周辺には面白い形の建物がたくさんあります。ピラミッドがビルの上に
乗っているもの、分度器がビルの屋上にあるものなど・・数学的なものが建物の中にも
たくさんありそうです。
【質問】
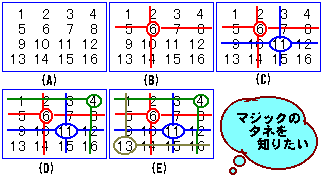
（Ａ）順番に番号が書かれているものを相手に見せて「なんだか３４が見える」という。
（Ｂ）相手の好きな番号を数値の中から言ってもらう相手がもし６番と答えたらその縦の列、
横の列の数値を消す。（赤い線のように）
（Ｃ）～（Ｅ）残った数字の中から選ばせて同じようにその数のある横列と縦列は消していく。
☆ すると、どうでしょう。勝手に選んできた数をたすと（６＋１１＋４＋１３のように）
始めに言った３４になっている。
なぜそうなるのですか？いつもですか。（文字式を使ってみると・・・もっといい説明は？）
【質問】
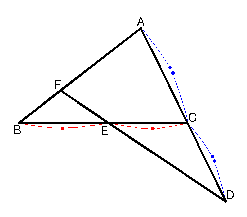
右のような図で CはADの中点で,EはBCの中点である。AF:BFを求めなさい。
（ヒント：補助線１本引けばわかる）
【質問】
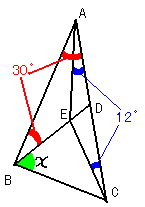
△ＡＢＣにおいて∠ＣＡＢ＝∠ＡＢＤ＝３０゜で∠ＣＡＥ＝∠ＡＣＥ＝１２゜である。
この時の∠Ｘの大きさを求めなさい。
（ヒントは正三角形をかいてみたらわかるかも）
【質問】
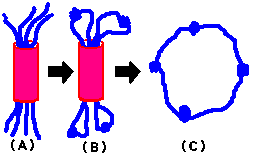
（Ａ）のように４本のひもが筒の中に入っている。筒の中はどうなっているのか
わからない状態である。
（Ｂ）のように上の４本のひもを２本ずつ結び、下も同じように結んだとき
（Ｃ）のように一つの大きな輪になる確率を求めてください。
（確率は結構高いんですね）
【質問】
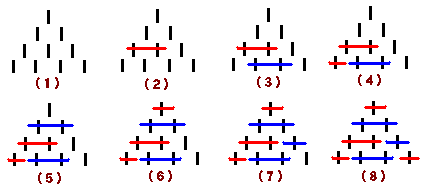
（１）のような図をノートなどに書いて始める。
（２）～（７）のように２人で交互に横線１本で黒の縦棒を消していく。消した棒に重なって消すことはできない。
（３）の時に１番下段の両側の縦棒を赤の方は１度に消すことはできない
（８）のように最後に縦棒を取り尽くしたほうが勝ち（このときは赤の勝ちである）
（三ッ山崩しというパズルに似ていますが、それよりも複雑で必勝法がわかりません）
|
